2001年4月22日更新（実習とレポートを見て追加）
関谷トップページへ 図形処理2001トップページへ 　

図形処理工学･図形処理実習No.1　科目概要とSLSによるグラフの作成

２００１．４．１６ 　　 KPC　情報技術科　関谷

1.「図形処理」の科目概要

　Ｃ言語やＪａｖａ言語（２Ｄ、３Ｄなど）、グラフィックスクライブラリ（ＯｐｅｎＧＬ，ＧＬＵＴなど）を使って、２次元、３次元のグラフィックス・プログラミングを学習します。
　Ｗｉｎｄｏｗｓの環境が使われるようになったので、それようのグラフィックスライブラリを扱うことになる。

　フリーソフトでは、Ｎ８８互換ＢＡＳＩＣ　for　Ｗｉｎｄｏｗｓ環境（潮田康夫）などでグラフィックスが使える。（ＭＳ−ＤＯＳの環境よりも、大変、便利になっている。）

　授業では、Ｃ言語でのプログラミングとして、平林雅著,Windows95プログラムを10倍簡単に作る（ＳＬＳ）をまず、実習する。
GLUTによる「手抜き」OpenGL入門,和歌山大学システム工学部 　床井浩平先生のhttp://www.sys.wakayama-u.ac.jp/~tokoi/opengl/libglut.htmlは、後半で実習する。

　次ぎに、オブジェクト指向のＪａｖａ２言語による図形処理プログラミングを、中山茂先生のテキストを参照して実習する。（中山茂、Ｊａｖａ２グラフィックスプログラミング入門、技報堂出版）

　なお、関谷のＷｅｂにあるＣＧ−図形処理工学−関連リンクは、Ｗｅｂページのいくつかを紹介している。
（この外によいＷｅｂページがあれば、皆さんから、小生へのメールを下さい。）

２．No.1　Windowsプログラミング、グラフィックスとSLSによるグラフの作成

2.1 プラットフォームと図形処理のライブラリ

図形処理のプログラムの中では，ｸﾞﾗﾌｨｯｸｽ機能を使います。
Window98でのVC++6 . 0 によるＣプログラミングのような開発環境（ハードウェアとオペレーティングシステムの組み合わせ）を，プラットフォームと呼んでいます。おなじ，プラットフォームでも，異なったコンパイラやインタプリタ、図形処理のライブラリが，いくつか使えます。

　Ｗｉｎｄｏｗｓ９８・ＮＴでのＣ＋＋コンパイラは，ＭＳ−ＶＣ＋＋のほかに，ＢｏｒｌａｎｄＣ＋＋などです。
　Ｎ８８互換ＢＡＳＩＣ　for　Ｗｉｎｄｏｗｓ環境（潮田康夫）もあります。
　ＵＮＩＸでは，Ｓｕｎや富士通のＣのほかに，ＧＮＵのｃなどのコンパイラが有ります。
　これらのコンパイラによっても，非互換が有ります。

Windowsでの図形処理を行うには、ＷｉｎｄｏｗｓのＡＰＩを使って、ハードウェアとのインターフェイスを取ることになりますが、図形処理そのものの部分は、その多くが行列の演算であるから、図形処理ライブラリができます。

　図形処理のライブラリとして、ＯｐｅｎＧＬがプラットフォームを選ばないで使えるようになっています。しかし、Ｗｉｎｄｏｗｓを開いたり・ハードウェアとのインターフェイスなど準備作業がプラットフォーム毎に必要で相当に面倒なため、その部分をＡｕｘ，Ｇｌｕｔなどのライブラリがサポートするようになっています。

「オブジェクト指向のプログラミング」では、クラスラブラリによる方法もある。しかし,従来の関数とは, 非互換になってしまう。
　　　　(MFC−Mircrosoft Foundation Class,とか工藤のLeaf for Windowsなどがある。)
　　　　(Java での2D, 3Dのグラフィックスなど）

2.2 Windows95/98/NT/2000でのＣ言語を使った簡単なグラフィックス・プログラムについて

( 参考書は平林雅著,Windows95プログラムを10倍簡単に作る,共立出版,1996.4.20初版から)

〔Ｗｉｎｄｏｗｓの仕組み〕

1−18 Windowsプログラムの仕組み（　Ｗｉｎ３２ＡＰＩ，ＭＦＣ−ＧＤＩ）
　（窓を自由に開いて，ＧＵＩでサポートするために，相当に忙しくなっています。）

1−19 10 倍簡単に作れる原理（ＳＬＳ）

◎プログラムの部品化−従来のMS-DOSでのグラフィックス関数(あるいは,BASICでのグラフィックス関数)に近い引数で使えるようにした。その関数仕様(引数と処理内容）については、sls\slsフォルダの*.fファイルを参照のこと。 

　　 p.50の枠内を参照（ＳＬＳ関数とその利用）
　　　　main()
　　　　｛
　　　　　　グラフィックスの初期化　gint();
　　　　　　グラフィックスの描写　　symbol();　　文字列の拡大
　　　　　　　　　　　　　　　　　　line(); 　　　直線
　　　　　　　　　　　　　　　　　　pset();　　　 点
　　　　　　　　　　　　　　　　　　circle();　　 円など
　　　　　　標準入出力も可能　　　　printf();　　コンソールへの表示
　　　　　　　　　　　　　　　　　　gets(); 　　　キー入力
　　　　　　グラフィックスの終了　　gend();
　　　　}

〔ＳＬＳの使い方〕 2章 p.63参照

1)コンパイルと実行のバッチファイル slsclg.batを用意する。内容は、以下のとおり。

CL /II:\sekiya\SLS\SLS %1.c %2 %3 %4 /link user32.lib gdi32.lib
if errorlevel 1 goto END
%1
:END

（\\c331sv03\read\sekiya\slsから,各自のホームディレクトリに コピーしてもよい。slsフォルダのパスをこのバッチファイルで指定している。)
注)　vc++へのパス(ｃｌ用)やdoskeyは、vcvars32.batなどでセットした後で、このバッチファイルを使う。
　sls フォルダには, #include " .f"で呼ぶファイルがある。それをｃｌで使えるようにしている。
なお、exe のフォルダには実行プログラムがあるので，サンプルの実行結果をすぐに見れる。( また, それぞれのソースプログラムは, BOOKのフォルダにある。)

2)コンパイルと実行は, １）で用意したバッチファイルslsclgを使う。
＞slsclg プログラム名　　（拡張子の．ｃを付けない）
　(注）　コンパイル時に、フォント名についてのワーニングが４件ほど出るが、実行できるので無視のこと。

2.3　 実習の課題とその要領

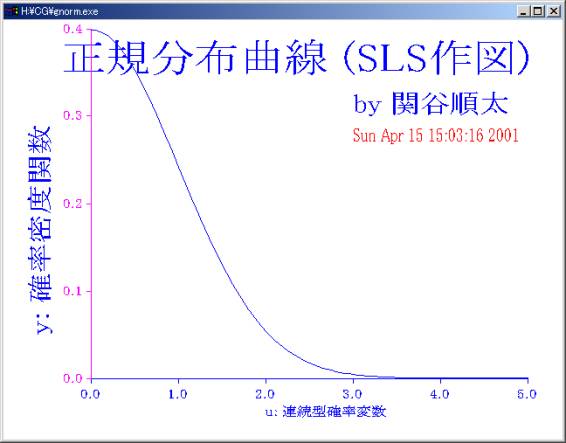
「正規分布曲線を,VC++6.0のコマンドラインコンパイラとSLSの関数等を使って, Windows2000で作図しなさい。（グラフの大きさ−対称にするとか−や、氏名、色などを変えてみること）」
(あるいは、皆さんの自由な作品でも良いです。作品の解説-目的や方法、仕組など-を付けて下さい。）
　小生の実行例を下に,参考のプログラム例を最後につけています。
提出資料は，ソースプログラムに考察を追加したものと,画面のハードコピーをWordに「貼り付け」、それを「Webページとして保存」したもの（HTML形式ファイルと画像圧縮したfilesフォルダのｊｐｇファイル）を、各自のＷｅｂページに表示すること。

注１）　画像の圧縮は、Wordでの圧縮を紹介したが、FrontPage　Expressやその他の圧縮機能があるソフトでよい。

注２) 画面のハードコピーとWordへの貼りつけ･保存の手順は以下のとおり。（サイズ等を変更したければ、Wordに貼りつける前にペイントで、編集などを行うことになる。）
　　 1 作図したグラフの画面をアクティブにします。(窓の選択です。)
　　 2 Alt キーを押したまま,PrintＳcreenキーを押して, クリップボードに取り込みます。
　　 3　Wordを起動して,カーソルを左上に移します。
　　 4　Wordで,編集−貼り付けを実行します。
　　 ５ Wordで, Myhome配下のフォルダに「Webページとして保存」を行う。圧縮された画像のファイルが同じファイル名.filesフォルダにあるので、それのうち、拡張子がjpgの方を使う。

注３）　Ｗｅｂページの作り方については、関谷のＷｅｂページの「個人ホームページの作成と更新」のページ（やWindows2000では、数値解析２０００１の最初の回のページの最後部）等を参照のこと。
　(ローカルのホームページフォルダは、c:\でなく、各自のサーバのﾎｰﾑ（H:)ドライブに作るのがよい。）
　作業としては、index_htmlフォルダの作成とそこでのindex_htmlファイルの変更−名前を表示したり、今回のページに対するリンクを作る−が必要になる。

実習とレポートを見て（2001.4.22）

「難しい、分からない」とき、どうしますか？

　皆さんのWebページ（レポート）を見ると、色や文字の大きさ,位置を変えている人が多かった。そして、「難しい、分からない」との感想もあった。

　新しい事（今回は、Windowsでのグラフィックスプログラミング）を学習しているのだから、最初は「難しい」とか「分からない」のは、当然ですよ。それを3時間ほどかけて、分かるようにしたいのです。どうしたら、分かるでしょうか？個人差もあるでしょうが、順番に（段階的に）、確認しながら、学習を進めることをしているのです。

  1. 授業で、きちんと、小生の資料を見たり、聞いていますか？まず、(何をどうしようとしているのか、どんな仕組なのかなど）聞く/調べる訓練をしましょう。
  2. 次には、自分の頭で、それらの仕組み・構造などを考えます。そして、言葉で書いてみます。それがレポートの考察になります。
  3. それから、プログラムの解析とプログラムの作成や改造です。

以上のような進め方で、再度、最初の回の学習を自分のものになるまで、復習しましょう。

SLSclg.batの使い方

　実習では、「コンパイルと実行」のバッチファイルSLSclg.batを紹介した。コンパイルでエラーのときでも、それを調べずに実行してしまうため、コンパイルエラー時は、前のプログラムがあればそれが実行される。これを避けるには、バッチファイルを以下のように変更のこと。
CL /II:\sekiya\SLS\SLS %1.c %2 %3 %4 /link user32.lib gdi32.lib
if errorlevel 1 goto END
%1
:END

実習課題のサンプル図とプログラム

SLSによる正規分布曲線の作図例

2001.4.15 KPC sekiya

SLSによる正規分布曲線の作図例

　

SLSを使ったグラフ作成プログラム例（gnorm.c)

/* gnorm.c  SLS によるWindowsでのグラフィックス 1996.4.25, 2001.4.15 time追加　 関谷*/ 
/*   平林雅英著、Windows95プログラムを10倍簡単に作る、共立出版,1996.4*/

#include <math.h>   /* for exp(), sqrt()  */
#include <stdarg.h> /* for sprintf() 数値を文字列に変換する */
#include <stdlib.h> /* EXIT_SUCCESS */
#include <time.h>

#include "gint.f"     /* グラフィックス初期化関数 gint,gend */
#include "line.f"     /* 線関数 */
#include "symbol.f"   /* 文字列拡大関数 */
#include "symbolv.f"  /* 縦書き文字列拡大関数(ｓｚ追加分) */
#include "rectfxor.f"   /* 長方形塗りつぶし関数 */

main()
{
  static int origx=100,origy=410;		/* 原点のスクリーン座標 */
  static int scalex=100,scaley=1000;    /* スクリーン座標の倍率 */
  int gx,gy, gxold, gyold;      		/* 点の座標 */
  double u, p, x, y ;    		/* u:確率変数、p:確率密度関数、軸の目盛り用*/
  int i;
  static double pai=3.141596;
  char *pa, axis_val[10];        /* *pa:日付用文字列(ポインタ変数）、axis_val:軸の目盛り数字 */
  long nowtime;

  time(&nowtime);
  pa = ctime(&nowtime);
  *(pa+24)='\0';
  printf("<%s>\n", pa);		/* 実行年月日・時間などをコマンドプロンプトに表示する。 */

gint(640,480); /* グラフィックス初期化(640x480dot) */
  symbol(50, 20," 正規分布曲線 (SLS作図)",6,3.,3.);
  symbol(400, 80,"by 関谷順太",6,2.,2.);
  symbol(400, 120, pa, 5,1.,1.5);
  line(origx,origy,origx+500,origy,6); /* Ｘ軸　x軸にyellow線を引く */
  line(origx,origy,origx,origy-400,4); /* Ｙ軸　y軸にgreen線を引く */

  for(i=0; i<101; i++){     /* 正規分布曲線の点座標計算と直線ｐｌｏｔ */
    u = 0.05*i; p = 1.0/sqrt(2.0*pai) * exp(-u*u/2.0);  
    gx = origx + scalex * u;
    gy = origy - scaley * p;
    if( i >0 )
        line(gxold,gyold,gx,gy,6);
    gxold = gx; gyold = gy;
  }

  for(i=0; i<6; i++){       /*  Ｘ軸目盛と数値　x axiss scale plot */
    x = i;			gx = origx + scalex * x;
    line( gx, origy, gx, origy+5, 6);
        sprintf(axis_val, "%3.1f", x);		/* 数値を文字列への変換　*/
        symbol(gx-12, origy+10, axis_val, 6, 1.,1.);
  }
  symbol( gx/2,origy+30, "u: 連続型確率変数", 6,1.,1.);
 
  for(i=0; i<5; i++){       /*  Ｙ軸目盛と数値　y axiss scale plot */
    y = 0.1 * i;	gy = origy - scaley * y;
    line( origx, gy, origx - 5, gy, 4);
        sprintf(axis_val, "%3.1f", y);
        symbol(origx-32, gy-8, axis_val, 4, 1.,1.);
   }
  symbolv(origx-75,origy-50, "y: 確率密度関数", 6,2.,2.);
	rectfillXOR(0,0,639,479,7);

  gend(); /* グラフィックス終了 */
  return EXIT_SUCCESS;
} /* main */        /** 終わり **/