図形処理･計算処理実習No.1　科目概要とSLSによるグラフの作成　　　　

２０００．４．１１　KPC　情報技術科　　関谷

1.「図形処理」の科目概要

　Ｃ言語やＪａｖａ言語（２Ｄ、３Ｄなど）、グラフィックスクライブラリ（ＯｐｅｎＧＬ，ＧＬＵＴなど）を使って、２次元、３次元のグラフィックス・プログラミングを学習します。
　Ｗｉｎｄｏｗｓの環境になったので、それようのグラフィックスを扱うことになる。

　フリーソフトでは、Ｎ８８互換ＢＡＳＩＣ　for　Ｗｉｎｄｏｗｓ環境（潮田康夫）などでグラフィックスが使える。（ＭＳ−ＤＯＳの環境よりも、大変、便利になっている。）

　授業では、Ｃ言語でのプログラミングとして、平林雅著,Windows95プログラムを10倍簡単に作る（ＳＬＳ）から,
GLUTによる「手抜き」OpenGL入門,和歌山大学システム工学部 床井浩平http://www.sys.wakayama-u.ac.jp/~tokoi/opengl/libglut.htmlをまず、実習する。

　次ぎに、オブジェクト指向のＪａｖａ２言語による図形処理プログラミングをテキストを参照して実習する。（中山茂、Ｊａｖａ２グラフィックスプログラミング入門、技報堂出版）

　なお、関谷のＷｅｂにあるＣＧ−図形処理工学−関連リンクは、Ｗｅｂページのいくつかを紹介している。
（この外によいＷｅｂページがあれば、皆さんから、小生へのメールを下さい。）

２．Windowsプログラミング、グラフィックスとSLSによるグラフの作成

2.1 ( 演習) プラットフォームと図形処理

図形処理では，の中でも，ｸﾞﾗﾌｨｯｸｽ を使います。
Window98でのVC++6 . 0 によるＣプログラミング,そこのような開発環境（ハードウェアとオペレーティングシステムの組み合わせ）を，プラットフォームと呼んでいます。おなじ，プラットフォームでも，異なったコンパイラやインタプリタ、図形処理のライブラリが，いくつか使えます。

　Ｗｉｎｄｏｗｓ９８・ＮＴでのＣ＋＋コンパイラは，ＭＳ−ＶＣ＋＋のほかに，ＢｏｒｌａｎｄＣ＋＋などです。
　Ｎ８８互換ＢＡＳＩＣ　for　Ｗｉｎｄｏｗｓ環境（潮田康夫）もあります。
　ＵＮＩＸでは，Ｓｕｎや富士通のＣのほかに，ＧＮＵのｃなどのコンパイラが有ります。
　これらのコンパイラによっても，非互換が有ります。

図形処理を行うには、ＷｉｎｄｏｗｓのＡＰＩを使って、ハードウェアとのインターフェイスを取ることになるが、図形処理そのものの部分は、その多くが行列の演算であるから、図形処理ライブラリに出来る。

　図形処理のライブラリとして、ＯｐｅｎＧＬがプラットフォームを選ばないで使えるようになっている。しかし、Ｗｉｎｄｏｗｓを開いたり・ハードウェアとのインターフェイスなど準備作業がプラットフォーム毎に必要で相当に面倒なため、その部分をＡｕｘ，Ｇｌｕｔなどのライブラリがサポートするようになった。

オブジェクト指向のプログラミングでは、クラスラブラリによる方法もある。しかし, 従来の関数とは, 非互換になってしまう。
　　　　　　　(MFC−Mircrosoft Foundation Class,とか工藤のLeaf for Windowsなどがある。)
　　　　　　　(Java での2D, 3D のグラフィックスなど）

2.2 Windows95/98/NTでのＣ言語を使った簡単なグラフィックス・プログラムについて

( 参考書は平林雅著,Windows95プログラムを10倍簡単に作る, 共立出版,1996.4.20初版から)

〔Ｗｉｎｄｏｗｓの仕組み〕
1−18 Windows プログラムの仕組み（　Ｗｉｎ３２ＡＰＩ，ＭＦＣ−ＧＤＩ）
（窓を自由に開いて，ＧＵＩでサポートするために，相当に忙しくなっています。）

1−19 10 倍簡単に作れる原理（ＳＬＳ）
　◎プログラムの部品化−従来のMS-DOSでのグラフィックス関数に近い引数で使えるようにした。
　　　　　　　　　　　　 (あるいは,BASICでのグラフィックス関数)
　　 p.50 の枠内を参照（ＳＬＳ関数とその利用）
　　　　main()
　　　　｛
　　　　　　グラフィックスの初期化　gint();
　　　　　　グラフィックスの描写　　symbol(); 　文字列の拡大　　　line(); 　　直線
　　　　　　　　　　　　　　　　　　　　　pset(); 　　点　　　　　　　　circle(); 　円など
　　　　　　標準入出力も可能 printf(); コンソールへの表示，gets(); 　キー入力
　　　　　　グラフィックスの終了 gend();
　　　　}

〔ＳＬＳの使い方〕 2章 p.63参照

1)バッチファイル slsclg.bat を用意する。内容は、以下のとおり。

CL /II:\sekiya\図形処理\SLS\SLS %1.c %2 %3 %4 /link user32.lib gdi32.lib
%1
（Infs02\read\sekiya\図形処理\slsから, 各自のディレクトリに コピーしてもよい。sls フォルダのパスをこのバッチファイルで指定している。)
注) sls フォルダには, #include " .f"で呼ぶファイルがある。
exe のフォルダでは, 実行プログラムがあるので，サンプルの実行結果をすぐに見れる。
( また, それぞれのソースプログラムは, BOOKのフォルダにある。)

2)コンパイルと実行は,
＞slsclg プログラム名　　（拡張子の．ｃを付けない）

2.3　 実習の課題とその要領

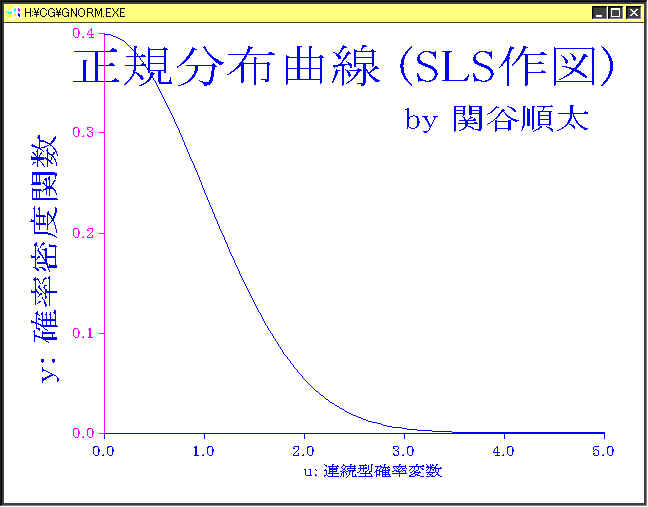
「正規分布曲線を,VC++6.0のコマンドラインコンパイラとSLS の関数等を使って, Windows98 で作図しなさい。（グラフの大きさや、氏名、色などを変えてみること）」
実行例を下に, 参考のプログラム例を最後に貼りつけています。
提出資料は，ソースプログラムに考察を追加したものと, 画面のハードコピーをFrontPage　Expressにまとめ、それを（HTML形式で）保存したものを、各自のＷｅｂページに表示すること。 （FrontPage　ExpressはプログラムのInternet　Exploreの次にある。）

注１) 画面のハードコピーとFrontPageへの貼りつけ･保存の手順は以下のとおり。（窓全体なら、３−４は省略できる）
　　 1 作図したグラフの画面をアクティブにします。( 窓の選択です。)
　　 2 Alt キーを押したまま,PrintＳcreen キーを押して, クリップボードに取り込みます。
　　 3　アクセサリのペイントを起動して, カーソルを左上に移します。( 既にある場合は, すべてを選択して, 切り取り( 削除) してから, 上記の 2をすること。カーソルの移動をします)
　　 4　ペイントで, 編集−貼り付けを実行します。
　　 5 次に, このなかの必要部分の図を, 選択・コピーします。
　　 6 FrontPageに貼り付ける。大きさや配置などが変更できます。
　　 7 FrontPageで, Myhome配下のフォルダにHTML形式で保存を行う。「改行のある普通の段落」とする。画像のファイルも同じフォルダに保存する。

注2）　Ｗｅｂページの作り方については、関谷のＷｅｂページの「個人ホームページの作成と更新」のページを参照のこと。
(ローカルのホームページフォルダは、c:\でなく、各自のサーバのﾎｰﾑ（H:)ドライブに作ること。）
　作業としては、index_htmlフォルダの作成とそこでのindex_htmlファイルの変更−名前を表示したり、今回のページに対するリンクを作る−が必要になる。

SLSによる正規分布曲線の作図例

2000.4.11 KPC sekiya

main()
{
  static int origx=100,origy=410;		/* 原点のスクリーン座標 */
  static int scalex=100,scaley=1000;    /* スクリーン座標の倍率 */
  int gx,gy, gxold, gyold;      		/* 点の座標 */
  double u, p, x, y ;    		/* u:確率変数、p:確率密度関数、軸の目盛り用*/
  int i;
  static double pai=3.141596;
  char axis_val[10];            /* 軸の目盛り数字 */

  gint(640,480); /* グラフィックス初期化(640x480dot) */
  symbol(50, 20," 正規分布曲線 (SLS作図)",6,3,3);
  symbol(400, 80,"by 関谷順太",6,2,2);
  line(origx,origy,origx+500,origy,6); /* Ｘ軸　x軸にyellow線を引く */
  line(origx,origy,origx,origy-400,4); /* Ｙ軸　y軸にgreen線を引く */

  for(i=0; i<101; i++){     /* 正規分布曲線の点座標計算と直線ｐｌｏｔ */
    u = 0.05*i; p = 1.0/sqrt(2.0*pai) * exp(-u*u/2.0);  
    gx = origx + scalex * u;
    gy = origy - scaley * p;
    if( i >0 )
        line(gxold,gyold,gx,gy,6);
    gxold = gx; gyold = gy;
  }

  for(i=0; i<6; i++){       /*  Ｘ軸目盛と数値　x axiss scale plot */
    x = i;			gx = origx + scalex * x;
    line( gx, origy, gx, origy+5, 6);
        sprintf(axis_val, "%3.1f", x);		/* 数値を文字列への変換　*/
        symbol(gx-12, origy+10, axis_val, 6, 1,1);
  }
  symbol( gx/2,origy+30, "u: 連続型確率変数", 6,1,1);
 
  for(i=0; i<5; i++){       /*  Ｙ軸目盛と数値　y axiss scale plot */
    y = 0.1 * i;	gy = origy - scaley * y;
    line( origx, gy, origx - 5, gy, 4);
        sprintf(axis_val, "%3.1f", y);
        symbol(origx-32, gy-8, axis_val, 4, 1,1);
   }
  symbolv(origx-75,origy-50, "y: 確率密度関数", 6,2,2);
	rectfillXOR(0,0,639,479,7);

  gend(); /* グラフィックス終了 */
  return EXIT_SUCCESS;
} /* main */        /** 終わり **/