俀侽侽侽丏俆丏侾俈丂KPC丂忣曬媄弍壢丂丂娭扟
丂椗慄傪昞帵偡傞妏搙傗丄摿掕偺妏搙偺慄偺怓傪曄偊傞偲偐丄幚尡傪偟偰傒傞偲丄僾儘僌儔儉偺夝愅偑偱偒偰椙偄丅
丂夞揮懱寫虃虛茙﹤虄f乕僞傪嶌傞偙偲偱丄棫懱偺僨乕僞偲偦偺搳塭偑傛偔暘偐傞丅(撶揷偝傫傗曮枮偝傫偺峫嶡偐傜乯
丂棫懱偺婎杮恾宍偱丄斾妑揑娙扨偵嶌傟傞傕偺偼丄悕懱丄拰懱丄夞揮懱偑偁傞丅
丂夞揮懱偼丄抐柺偺2師尦恾宍傪丄y幉偺夞傝偵夞揮偝偣傞偙偲偵傛傝惗惉偱偒傞丅
丂偦傟偩偗偱偼丄暋悢屄偺懭墌偑昤偗傞偩偗偱丄偲偰傕棫懱偵偼尒偊側偄丅偦偙偱丄抐柺傪昞偡捈慄乮椗慄乯傪偁傞夞揮妏搙偛偲偵壗売強偐偵昤偔偙偲偵偡傞丅
丂倶幉夞傝偺夞揮検-夞揮偺岦偒乮晞崋乯-偼娭學偟側偄偙偲偵側傞丅乮搳塭懳徾偺夞揮懱偑倷幉偵懳徧側偨傔乯堿塭傪晅偗側偄応崌丄搳塭恾偐傜偼丄倶幉夞傝偺夞揮偺岦偒傪偳偪傜偐嬫暿偱偒側偄丅
丂
丂偙傟偼丄夞揮懱偲堘偄丄倶幉夞傝偺夞揮検-岦偒乮晞崋乯-偼搳塭恾偱敾暿偱偒傞丅
僌儔僼傿僢僋僗偺悽奅傪夝愅揑偵昞尰偣偢丄嵞婲揑偵昞尰偡傞丅
儕僇乕僔僽丒僌儔僼傿僢僋僗偺偍傕偟傠偝偼丄嬃偔傎偳帺慠偺宍偵嬤偄恾宍偑偄偲傕娙扨偵昞尰偱偒丄帺慠傗惗柦偺恄旈揑側旤偟偝傪夝偒柧偐偣傞偺偱偼側偄偐偲偄偆嶖妎傪闂闇偲偝偣傞偲偙傠偵偁傞丅
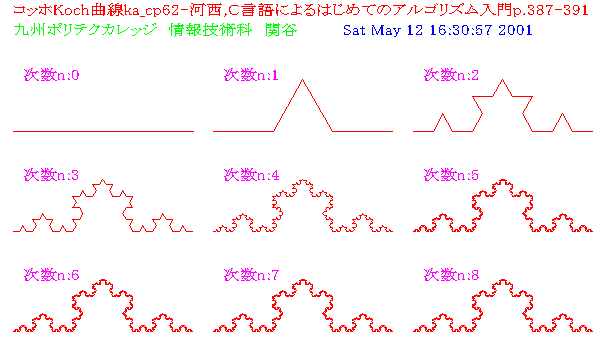
丂崱夞偼丄壨惣偺俉丏俀丄俉丏俁偐傜丄椺戣俇俀丂僐僢儂嬋慄偲椺戣俇俁丂庽栘嬋慄傪妛廗偡傞丅
丂侽師偺僐僢儂嬋慄偼挿偝倢偺捈慄偱偁傞丅侾師偺僐僢儂嬋慄偼丄侾曈偺挿偝偑l/3偺戝偒偝偺惓3妏宍忬偺弌偭挘傝傪弌偡丅2師偺僐僢儂嬋慄偼丄侾師偺僐僢儂嬋慄偺奺曈偵懳偟丄侾曈偺挿偝偑l/9偺戝偒偝偺惓3妏宍忬偺弌偭挘傝傪弌偡丅偙傟傪柍尷夞孞傝曉偣偽丄柍尷彫偺挿偝偺慄暘偑柍尷杮偮側偑偭偨嬋慄偲側傞丅
丂師悢偼丄侽偐傜俉師傑偱偺9恾傪3抜偵側傜傋偨丅 丂偙偺偨傔偵偼丄window(), view()偺娭悢傪巊偄丄孞傝曉偟傪峴偭偰偄傞丅

椺戣俇俀丂僐僢儂嬋慄傪昞帵(侾 View)
丂庽栘嬋慄偼丄栘偑巬傪怢偽偟偰偄偔宍傪偟偨恾宍偱偁傞丅
丂師偺婯懃偵廬偆丅
丂庽栘嬋慄偼丄恊偺巬偐傜2杮偺巕偺巬傪弌偟偰偄偔偺偱丄2暘栘偺栘峔憿偲傑偭偨偔摨偠偲峫偊傞偙偲偑偱偒傞丅
丂値師偺栘傪昤偔傾儖僑儕僘儉偼師偺傛偆偵側傞丅
侾乯乮倶0,倷0乯偐傜妏搙angle偱挿偝leng偺巬傪侾偮堷偔丅堷偒廔傢偭偨揰偺嵗昗傪怴偟偄乮倶0,倷0乯偲偡傞丅
俀乯値亅侾師偺塃晹暘栘傪嵞婣屇傃弌偟
俁乯値亅侾師偺嵍晹暘栘傪嵞婣屇傃弌偟
丂師悢n丄妏搙branch丄弅彫棪scale偼丄僉乕僀儞偡傞丅 丂3慻傪僗僋儕乕儞偱偼丄廲偵暲傋偰昞帵偡傞丅 丂3慻傪昞帵偟偨傜丄怓偺斀揮傪偡傞丅

椺戣俇俁丂庽栘嬋慄傪昞帵(3 View)
丂
儕僇乕僔僽丒僌儔僼傿僢僋僗偺僾儘僌儔儉傪夝愅偟側偝偄丅
師偵偦傟傜傪夵憿偟丄嶌昳傪嶌傝側偝偄丅
椺乯庽栘偺僨乕僞丒怓側偳傪曄偊傞丅攝抲傪曄偊傞丅乮椦偵側傞丠乯
侾乯Word偁傞偄偼FrontPageExpress偵丄峫嶡丄僜乕僗儕僗僩丄幚峴僌儔僼傿僢僋僗夋柺傪揬傝晅偗偨傕偺傪乽Web儁乕僕乿偺宍幃(奼挘巕偼html)偱丄奺帺偺MyHome偵丄cg_05側偳偺柤慜傪偮偗偰曐懚偡傞丅
俀乯忣曬宯Web僒乕僶偑丄Turbolinux偱嵞峔抸偝傟偨偺偱丄偦偺Web儁乕僕偵index.html偐傜偺僴僀僷乕儕儞僋傪嶌偭偰丄搊榐偡傞丅(拲傪嶲徠偺偙偲丅奣棯偼埲壓偺偲偍傝丅乯乯
丂html僼傽僀儖偼丄Word傗FrontPageExpress側偳偱丄Web儁乕僕偲偟偰曐懚偡傞(慜弎乯丅偦偟偰丄儂乕儉儁乕僕index.html偐傜丄崱夞偺儗億乕僩儁乕僕傊偺儕儞僋傪挘傞丅偦傟傜傪奺帺偺Web僒乕僶偺儂乕儉僨傿儗僋僩儕偺捈偖壓偺public_html僼僅儖僟乮僒僽僨傿儗僋僩儕乯偵ftp偡傞偙偲丅
丂
拲乯丂倂倕倐儁乕僕偺嶌傝曽偵偮偄偰偼丄娭扟偺倂倕倐儁乕僕偺乽屄恖儂乕儉儁乕僕偺嶌惉偲峏怴乿偺儁乕僕傪嶲徠偺偙偲丅乮Web僒乕僶偺嵞峔抸偑姰椆偟偨丅乯
(側偍丄儘乕僇儖偺儂乕儉儁乕僕僼僅儖僟偼丄c:\偱側偔丄奺帺偺僒乕僶偺伟褋iH:)僪儔僀僽偵嶌傞偙偲丅乯
丂嶌嬈偲偟偰偼丄public_html僼僅儖僟偱偺index_html僼傽僀儖偺曄峏亅柤慜傪昞帵偟偨傝丄崱夞偺儁乕僕偵懳偡傞儕儞僋傪嶌傞亅偑昁梫偵側傞丅