2000.4.19 KPC 情報技術科 関谷
MS-DOS版 C言語コンパイラのグラフィックス関数の違いを吸収して、12個の標準ライブラリ関数とその仕様を、河西朝雄が1992年5月に決めた。(河西朝雄、C言語によるはじめてのアルゴリズム入門、技術評論社、1992.5.25初版、第8章-pp.313-408)
Glib.hの主な特徴は次の3点である。
そのGlib.hを使って、河西は以下の機能を実現している。
詳細は、テキストを参照のこと。
なお、河西は、「Visual Basicによるはじめてのアルゴリズム入門」(1999年6月、技術評論社刊)8章グラフィックスで、VBでのWindowsグラフィックスを示している。
Slsは平林によるWindows グラフィックス用のライブラリである。(No.1の平林雅著,Windows95プログラムを10倍簡単に作るを参照)。
Slsの上に、上記の河西のGlib.hを移植したものが、Glibwv.hグラフィクス・ライブラリである。MoveとTurn、2D、3Dなどのグラフィックス・プログラミングが、Windows上で実現できる。
図形処理の基本プログラム例として、
1)Move とTurnでは、例題56 正n角形を描く(n=3〜9)
練習問題56 渦巻き模様
2)2次元座標変換では、例題57 対称図形
練習問題57 回転・拡大コピー
を紹介する。
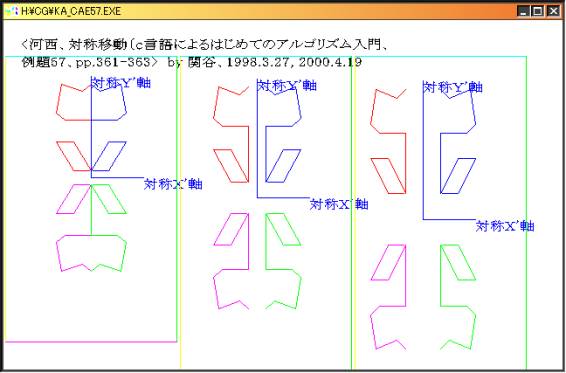
対称複写をビューを使って同じ描画を繰り返した例
例題を参考に、皆さんの描きたい図形データなどを用意して、プログラムを改造し、作品を作りなさい。
Wordに、考察、ソースリスト、実行グラフィックス画面を貼り付けたものを「Word文書」の形式で保存したファイル(ファイル名は、学籍番号2桁_02.doc)を、ファイルサーバ(R:\sekiya\図形処理\No02_Gl1に提出のこと。
注1) 画面のハードコピーとWordへの貼りつけ・保存の手順は以下のとおり。(窓全体なら、3−4は省略できる)
1 作図したグラフの画面をアクティブにします。(窓の選択です。)
2 Alt キーを押したまま,PrintScreen
キーを押して, クリップボードに取り込みます。
3 アクセサリのペイントを起動して,カーソルを左上に移します。( 既にある場合は,すべてを選択して, 切り取り( 削除) してから,
上記の 2をすること。カーソルの移動をします)
4 ペイントで,編集−貼り付けを実行します。
5 次に, このなかの必要部分の図を,選択・コピーします。
6 Wordに貼り付ける。大きさや配置などが変更できます。
7 Wordで, 文書として各自のホームドライブの科目のフォルダに、名前を付けて保存する。
注2) Webページの作り方については、関谷のWebページの「個人ホームページの作成と更新」のページを参照のこと。(現在、Webサーバのバージョンアップ中で使えない。)
(ローカルのホームページフォルダは、c:\でなく、各自のサーバのホーム(H:)ドライブに作ること。)
作業としては、index_htmlフォルダの作成とそこでのindex_htmlファイルの変更−名前を表示したり、今回のページに対するリンクを作る−が必要になる。
// Glibwv.h 河西朝雄、C言語によるはじめてのアルゴリズム入門、pp.346-356 からSLSを使用して、Windows用に移植。 // 1998.3.16 北九州職業能力開発短期大学校 情報処理科 関谷順太
#include <math.h>
#include "line.f"
#include "pset.f"
#define pset(x,y,c) \
WvLine((double)(x),(double)(y),(double)(x),(double)(y),(int)c)
#define window(x1,y1,x2,y2) \
Window((double)(x1),(double)(y1),(double)(x2),(double)(y2))
#define view(x1,y1,x2,y2) \
View((int)(x1),(int)(y1),(int)(x2),(int)(y2))
#define setpoint(x,y) \
SetPoint((double)(x),(double)(y))
#define setangle(a) \
ANGLE=(double)(a)
#define turn(a) \
ANGLE=fmod(ANGLE+(a), 360.0)
#define move(l,c) \
Move((double)(l), (int)(c))
#define moveto(x,y,c) \
MoveTo((double)(x),(double)(y),(int)(c))
#define moverel(x,y,c) \
MoveTo((double)(LPX+(x)),(double)(LPY+(y)), (int)(c))
#define wvline(x1,y1,x2,y2,c) \
WvLine((double)(x1),(double)(y1),(double)(x2),(double)(y2),(int)(c))
double ANGLE, /* 現在角 */
LPX, LPY; /* 現在位置 */
//int C=1; /* 色 */
double WX1,WY1,WX2,WY2, /* ワールド座標 */
VX1,VY1,VX2,VY2, /* ビュー座標 */
FACTX,FACTY; /* スケール */
int PX1,PY1, PX2, PY2; // 現在スクリーン座標
int Cpy(void){
return PY2;
}
int Cpx(void){
return PX2;
}
void Window(double x1, double y1, double x2, double y2)
{
WX1=x1; WY1=y1; WX2=x2; WY2=y2;
FACTX=(VX2-VX1)/(WX2-WX1);
FACTY=(VY2-VY1)/(WY2-WY1);
}
void View(int x1, int y1, int x2, int y2)
{
VX1=(double)x1; VY1=(double)y1; VX2=(double)x2; VY2=(double)y2;
FACTX=(VX2-VX1)/(WX2-WX1);
FACTY=(VY2-VY1)/(WY2-WY1);
}
void WvLine(double x1, double y1, double x2, double y2, int c)
{
PX1 = (int)((x1-WX1)*FACTX+VX1);
PY1 = (int)((y1-WY1)*FACTY+VY1);
PX2 = (int)((x2-WX1)*FACTX+VX1);
PY2 = (int)((y2-WY1)*FACTY+VY1);
line(PX1, PY1, PX2, PY2, c);
// LPX=x2; LPY=y2;
}
void Move(double l, int c)
{
double x,y,rd=3.14159265359/180.0;
x=l*cos(rd*ANGLE); y=-l*sin(rd*ANGLE);
WvLine(LPX, LPY, LPX+x, LPY+y, c);
LPX += x; LPY +=y;
}
void MoveTo(double x, double y, int c)
{
WvLine(LPX, LPY, x, y, c);
LPX = x; LPY =y;
}
void SetPoint(double x, double y)
{
LPX=x; LPY=y;
}
/* ka_cap57.c 2次元座標変換 p.364-5 1998.3.27 sekiya */
#include <stdlib.h> /* EXIT_SUCCESS */
#include "gint.f" /* グラフィックス初期化関数 gint,gend */
#include "basescrn.f" /* 基本画面設定関数 base_screen */
#include "line.f" /* 直線関数 */
#include "gcls.f" /* 消去関数 */
#include "symbol.f" /* 文字関数 */
#include "Glibwv.h" /* タートル関数Glibwv.h(河西) */
void multi(double fx, double fy, double *x, double *y); // change size
void rotate(double angle, double *x, double *y); // 回転移動
main(int argc,char *argv[])
{
static double xo[]={ 0., 100.,100., 0., 0.},
yo[]={ 0., 0.,200., 200., 0.};
double x[5], y[5], fx=0.6, fy =0.6, angle= 15.0;
int i, j, k, imax=3, vxl=0, vxr=200, vxd=200, n=5;
printf("Ctrl+Cで終ります。\n");
if(argc==1)
{ /* 引数なし(標準) */
gint(640,400); /* グラフィックス初期化(640x400dot) */
}
else
{ /* 引数あり(拡大) */
gint(1000,625); /* グラフィックス初期化(1000x625dot) */
base_screen(640,400); /* 基本画面設定 */
}
gcls();
window(- 70, -280, 130, 120);
symbol(20,20,"<河西、回転移動(c言語によるはじめてのアルゴリズム入門、",7,1,1);
symbol(20,40,"練習問題57、pp.364-365> by 関谷、1998.3.27, 2000.4.19",7,1,1);
for(i=0; i<3; i++){
view(vxl,370+33*i, vxr,40); // ビューポートの設定
printf("angle:%5.0f, fx:%5.1f, fy:%5.1f\n", angle, fx, fy);
for(j=0; j < n; j++) {
x[j] = xo[j]; y[j] =yo[j];
if (j==0)
setpoint(x[j],-y[j]);
else
moveto(x[j],-y[j], 6);
}
for(j=0; j<12; j++) {
for(k=0; k < n; k++) {
}
for(k=0; k < n; k++) {
multi(fx, fy, &x[k], &y[k]); // x,y座標値の拡大・縮小
rotate(angle, &x[k], &y[k]); // x,y座標値の回転
if (k==0)
setpoint(x[k],-y[k]);
else
moveto(x[k],-y[k], 7);
}
}
// y axiss plot
setpoint(0., 0.);
moveto(0, -220.0, 6);
symbol(Cpx(), Cpy(), "Y'軸",6,1,1);
// x axiss plot
setpoint(0., 0.);
moveto(110.0, 0.0 , 6);
symbol(Cpx(), Cpy(), "X'軸",6,1,1);
// view を描く
wvline(-49,-99,-49,99,1); // blue left line
wvline(-49, 99, 49,99,2); // red uper line
wvline( 49, 99, 49,-99,3); // purple right line
wvline( 49,-99,-49,-99,4); // green lower line
vxl += vxd; vxr += vxd;
angle += 15.0;
fx += 0.10; fy += 0.10;
}
gend(); /* グラフィックス終了 */
return EXIT_SUCCESS;
} /* main */
void multi(double fx, double fy, double *x, double *y) // change size
{
*x = fx *(*x);
*y = fy *(*y);
}
void rotate(double deg, double *x, double *y) // 回転移動
{
double dx, dy, rd=3.14159/180;
deg *= rd;
dx = (*x)*cos(deg) - (*y)*sin(deg);
dy = (*x)*sin(deg) + (*y)*cos(deg);
*x = dx; *y = dy;
}