�i�k��B�E�ƌP���Z����w�Z�I�v�@��4���@pp.29-36�@1992�N3���j
�@�k��B�E�ƌP���Z����w�Z�@����ȁ@�֒J�@����
�@�@�@�@�ڎ� �v�� �P�D�͂��߂� �Q�D�h�r�l�@�ɂ��� 2.1 �@�h�r�l�@�̊T�v 2.2 �@�h�r�l�@�̌v�Z���� 3. �h�r�l�\���w�K�@�ƃ\�t�g�ɂ��� 3.1 �h�r�l�\���w�K�@ 3.2 �h�r�l�\���w�K�@�p�\�t�g 4. �v���O�����̎���ƌ��� 4.1 �אڍs��ɂ��K�w�v�Z�v���O���� 4.2 �אڃ��X�g�ɂ��K�w�v�Z�v���O���� 4.3 �K�w�}�̃v�����^�o�̓v���O���� 5. �l�@ 6. ������ �Q�l���� 2002.3.22 �A�b�v���[�h���̕⑫
�@�h�r�l(Interpretive Structural Modeling)�|�킩��₷���\�����@�|5)�́A�Љ�V�X�e���H�w�̕���ɂ����āA���G�ŕs���m�Ȗ��ɑ��āA���낢��ȗv�f�Ԃ̑��݊W�𑽊K�w�̗L���O���t�Ƃ��Đ}�����āA���f���̉��߂ƌ������s�����̂ł���B����2)�͂�������ޓ��e�̍\�����̖��ɓK�p���u�h�r�l���ލ\�����@�v���Ă��A���p���L�������B�\�����f���̍쐬�ɂ́A�R���s���[�^���g���ƕ֗��ł���A���{�d�C�\�t�g�E�F�A�i���j6)���o�b�X�W�O�O�V���[�Y�p�\�t�g��̔����Ă���B
�@�k��B�E�P�Z��̏���ȃJ���L�������u�f�[�^�\��II�v�ɂ�����O���t�̋��ނƂ��Ă̗��p���l���āA�h�r�l�@�ł̊K�w�v�Z��אڃ��X�g�ōs���v���O�������p�\�R���e�l�|�q�̂a�`�r�h�b�Ŏ��삵���B�אڍs��ł̏������Ԃ��v�f���̂Q��ɔ�Ⴗ��̂ɑ��āA���̗אڃ��X�g�ł́A�v�f���ɔ�Ⴗ��B�������Ԃ́A�v�f�����P�X�łP�S�O�b�R�b�ł���B
�@�\���}�i�g�ƃ��x���j�̃v�����g�v���O�������쐬�������A���݂̒i�K�ł͂܂��l���K�w�\�Ɨאڃ��X�g�����āA�K�w���Ƃ̗v�f�̕��т���͂��Ȃ���͂Ȃ�Ȃ��B
�����̃v���O�������g���āA���ށE�J���L�������̂ق����낢�땡�G�Ȗ��̍\�������A�Q���^�V�X�e���Y�E�A�v���[�`�ōs�����Ƃ��ł���B
�@������̑傫�ȃe�[�}�̈�̓J���������E���ނł���B�����̍쐬�@�ɂ��āC����1)�̉�����w�Z�\�ƋZ�p�x�R�^�P�X�X�P�ɁA�u�R���Z�v�g�E�}�b�s���O�A�v���[�`�ɂ�鋳�ފJ���v�Ƃ��Ă���B����Ɉ��p���ꂽ�Q�l����2,3)�ɂ��A�h�r�l�\���w�K�@�́A�M�҂��W���Đ��N�O�ɊJ�������\�t�g�E�F�A�u�A�}�Ƃc�d�l�`�s�d�k�̃p�\�R�������V�X�e���r�`�l�c�h�b�|�o(Systems Aproach by Matrix Development on Inter-related chart with Personal computers)�v4)�Ɨގ������\�t�g�E�F�A���g���BSAMDIC-P�́A�d�ݕt���̂Q���W����A�K�w�}��v���̑w�ʐ}�i�֘A�x�C�e���x�j��������Ă����@�\�����B
�@���Z����ł́A�p�\�R���p�\�t�g�u�h�r�l�\���`���[�g�쐬�V�X�e���i�h�r�l�|�X�W�j�v5)���w�����Ă��Ȃ������B���̃\�t�g�����Ƃ��Ă��A�����Ŏ��R�ɉ����ł��Ȃ��B�i���̌ケ�̃\�t�g�͍w�����ꂽ�B)
�@���Z�����Ȃ̃J���L�������u�f�[�^�\��II�v�̎��Ɨ\��ɃO���t������A���̒��ɂ͗אڍs��Ɨאڃ��X�g�̔�r��g�|���W�J���\�[�g�̃v���O����7)���������B�����ŁA�����̓��e�Ɋւ���v���O���~���O�ɂ��m�F��ƂƂ��Ẵv���O�������p�\�R���e�l�q�|�U�O�Ŏ��삵�A���̃v���O���������ނ̈�Ƃ����B
�@���̃v���O�����͋��ޓ��̋��番��݂̂łȂ��A��ʂ̖��\���̗����ɖ𗧂�@�E����( �c�[��) �ł���̂ŁA�����ɕ���B
�@�h�r�l�@5)�́A�A�����J�̃o�e���E�R�����o�X�������ŊJ������A�L���g�p�����悤�ɂȂ����\�����f�����O��@�̂ЂƂł���B
�@���̎�@�́A�R���s���[�^��}��Ƃ��āA����ꂪ�S�̒��ɕ����Љ���Ƃ̕��G�Ȗ��̃C���[�W���A�V�X�e���\���v�f�̈�Δ�r�ɂ���Ė��m�Ȏp�Ƃ��ĕ����яオ�点�A�S�̑�����ڂŔc�������悤�Ƃ�����̂ł���B�\�����f���A���Ȃ킿�v�f�Ԃ̑��݊W�p�^�[���́A�uInterpretive Structural Model �v�ƌĂ�鑽�K�w�̗L���O���t�Ƃ��Đ}������C���ꂪ�Ăѐl�Ԃ̒��ς�z���͂��h�����Ė��̖{���ɔ���Ƃ������̃}���E�}�V���n�𐬂��Ă���B
�@�\�����͎�@�̓����́A���G�ŕs���m�Ȗ��ɑ��āA���̗v�f�E�\���E�͈́E���e�Ȃǂ����R�Ƃ����i�K����o�����Ď���ɖ��𖾂炩�ɂ��Ă����ߒ����̂��̂ɂ���B���̉ߒ��ɂ͈�ʂɁA
�i�P�j�\���v�f�̒��o �i�Q�j�v�f�Ԃ̊W�Â� �i�R�j�\�����f���̍쐬 �i�S�j���f���̉��߂ƌ��� �Ƃ����菇���܂܂��B
�@�h�r�l�@�́A�O���t���_�̊�{�I�T�O���R���s���[�^��}��Ƃ��Čn���I�ɓK�p���邱�Ƃɂ��A���낢��ȗv�f�Ԃ̑��݊W�p�^�[�����h�r�l�ƌĂ�鑽�K�w�̗L���O���t�Ƃ��Đ}������B
�@���ׂ̈̃R���s���[�^�E�\�t�g�ł̏����菇�́A�Q�D�P�ɏq�ׂ��菇�ƑΉ����Ď��̂悤�ɂȂ�B
�i�P�j�v�f�̒�` �i�Q�j�Q���W�̓��� �i�R�j�אڍs��̍쐬�@�@�i�אڃ��X�g�쐬�j �i�S�j���B�s��̌v�Z���i�K�w�v�Z�Əo�́j �i�T�j���x�������Əo�̈́� �i�U�j���i�s��̌v�Z �i�V�j�ŏ��ӗL���O���t�̍쐬
�@����ߒ��̕Ґ��͋��ȓ��e�̊�b�I�\�����\���ɔ��f�������̂łȂ��Ă͂Ȃ�Ȃ��B���̂��߂ɂ͋��t�͋���ߒ��E�w�����e�̕Ґ��ɓ������āA���̋��ȓ��e�̊�b�I�\���͂��������Ă������Ƃ��K�v�ł���B
�@�������m2,3)�́A�h�r�l�@�Ƌ��ޓ��e�̍\�����̖������т��āA�h�h�r�l���ލ\�����@�h���Ă��A�����̎����̂̋���Z���^�[��C�O�̑�w�ɂ܂ŕ��y�����Ă��Ă���Ƃ����B���̊w�K�@�́A�p�\�R���̕��y�ɂ���Ď��p������i�ƍ��܂��Ă���B
�@�h�r�l�\���w�K�@�p�\�t�g�Ƃ��ẮA�u���ލ\���`���[�g�쐬�V�X�e���@�h�r�l�|�X�W�v���m�d�b�p�[�\�i���R���s���[�^�o�b�|�X�W�O�O�V���[�Y�p�ɁA���{�d�C�\�t�g�E�F�A������A�艿100,000 �~�Ŕ̔�����Ă���B�i�m�d�b�ȊO�̂e�l�p�Ȃǂ͂Ȃ��B�j ���̃\�t�g�́A
�@�i�P�j�^�p���� �@�i�Q�j���ޗv�f�̓o�^�E�lj��E�C�� �@�i�R�j���ލ\���`���[�g�̍쐬�E�~�� �@�i�S�j���ލ\���`���[�g�̌��� �@�i�T�j���[�e�B���e�B
�Ȃǂ̋@�\�������A���j���[�ɏ]���āA���S�҂ł��g����悤�ɂȂ��Ă���B
�����Ƃ��āA�ӂ̌��������Ȃ��Č��₷���z�u�̍\���`���[�g�������I�ɍ���ق��A���ԃf�[�^���������}����邱�Ƃ��ł���B
�����\�ȃf�[�^���́A���̂Ƃ���ł���B
�P�j�ꖇ�̃f�[�^�f�B�X�N�ɓo�^���邱�Ƃ̂ł���v�f���F�X�X�X�ȓ� �Q�j��x�ɍ\�����̑ΏۂƂ��邱�Ƃ̂ł���v�f���F�U�O�ȓ� �R�j�ꖇ�̃f�[�^�f�B�X�N�ɓo�^���邱�Ƃ̂ł��鋳�ލ\���`���[�g���F�T�O�ȓ�
�@�R�D�Q�ɏq�ׂ������菇�ɂ���āA���x�������E�o��( �K�w�v�Z�E�o��) �܂ł̃v���O�����h�r�l�D�a�`�r��������B���̃v���O�����͗אڍs��E���B�s����g���A���x���������s�����̂ŁA�e�l�q�|�U�O�̂e�a�g�f�C���^�v���^�łR���Ԃقǂłł����B���̃v���O�����ł̌v�Z���Ԃ́A�v�f�����Q�V�Ȃ�U�`�W���Ƒ��������Ȃ邪�A�v�f�����P�X�Ȃ�Q�`�R���ŋ��܂�B
�@�Ȃ��A���B�s��̌v�Z�� Warshall �̃A���S���Y���i�O���t�̐��ړI��j8)���g�p���� ISMW.BAS �ł̌v�Z���Ԃ́A�v�f�����Q�V��41�b�A�v�f�����P�X��20�b�ŋ��܂�A�傫�����P���ꂽ�B
1)���̓f�[�^
�@�E���̓t�@�C����(MS-DOS �e�L�X�g�`��) �i�����C�k���Ȃ�ȉ��̃L�[�{�[�h����̓��͂Ƃ���B�t�@�C���́A�L�[�{�[�h���̓f�[�^�Ɠ������тƂ���B�j
�@�E���f�����Ɨv�f��
�@�E�v�f�ԍ��h�Ƃi�i�h���i�A�h���i�̑O��Ƃ��A�h���i�̗v���Ƃ��j�i���͂̍Ō�́A�O�C�O�Ƃ���B�j
�Q�j�o�̓f�[�^�i�b�q�s����уv�����^�j
�@�E���̓t�@�C����
�@�E�אڍs��
�@�E���B�s��
�@�E�K�w�f�[�^�\
�R�j��������Ȃ�
�@�E�v�f���F�S�O�ȉ�
�@�E�K�w���F�S�O�ȉ�
�@�E��̊K�w�ł̗v�f���F�S�O�ȉ�
�@�E���[�v�������Ă��悢�B
�S�j�s���F�P�P�O�i�R�����g���܂݃}���`���j
�T�j���s���}1 �ɂ��߂��B���̍\�����f���́i���j�ł���C���̓t�@�C�����i���j�C�v�����^�o�͂��i���j�ł���B
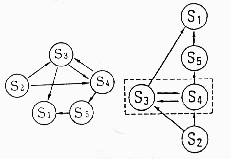
ISM�} 1-2 �C5 2 3 2 4 3 1 3 4 4 3 4 5 5 1 0 0
[�אڍs��ɂ��K�w�v�Z]�@91/12/28 �t�@�C�����Fismd124.dat [ISM�} 1-2]�C�v�f���F�@5�@15:56:08 �@�אڍs�� I/J 1 2 3 4 5 1 0 0 0 0 0 2 0 0 1 1 0 3 1 0 0 1 0 4 0 0 1 0 1 5 1 0 0 0 0 ���B�s�� M(i,j) 15:56:09 I/J 1 2 3 4 5 1 1 0 0 0 0 2 1 1 1 1 1 3 1 0 1 1 1 4 1 0 1 1 1 5 1 0 0 0 1 [ISM�} 1-2]�C�K�w�f�[�^�\�@15:56:10 ���x�� :�v�f�Q 1 : 1 2 : 5 3 : 3 4 4 : 2
[�אڃ��X�g�ɂ��K�w�v�Z]�@91/12/28 �t�@�C�����Fismd124.dat [ISM�} 1-2]�C�v�f���F�@5�@14:05:56 �@�אڃ��X�g I(�O��A�v��)�@[������][�o����]�@J(��A����) 1 [ 2][ 0] 0 2 [ 0][ 2] 3 4 3 [ 2][ 2] 1 4 4 [ 2][ 2] 3 5 5 [ 1][ 1] 1 [ISM�} 1-2]�C�K�w�f�[�^�\�@14:05:57 ���x�� :�v�f�Q 1 : 1 2 : 5 3 : 3 4 4 : 2
�@�u�f�[�^�\��II�v�̋��ȖڂŁA�O���t���w�K����B�����Ŏg�p�����e�L�X�g7)�W���ł́A�u�O���t�̕\���@�Ƃ��Ă̗אڍs��́A�v�f�Ԃ̊W���Ȃ����������a�ȍs��̏������A���Ԍv�Z�ʂ��n�i��2�j�ł����Č����������B�@����A�אڃ��X�g�ƌĂ����`���X�g���g���Ƃn�i���j�ł���C�������ǂ��B�v�ƌ��_�݂̂��q�ׂĂ���B�����āA���̗אڃ��X�g�̂��g���ăg�|���W�J���E�\�[�g��N���e�B�J���E�p�X�@�̃v���O�������b����ŗᎦ���Ă������B���̗אڃ��X�g�E�t�אڃ��X�g���g���ăg�|���W�J��������������A���S���Y�����Q�l�ɂ��āA�a�`�r�h�b�ł̓��X�g��z��ɂ��ĊK�w�v�Z���s�����B�쐬�͕ύX������ĂQ���Ԓ��x�ł���B
1)���̓f�[�^ �@�@5.1 �אڍs��ɂ��v���O�����i�h�r�l) �ɓ����B �Q�j�o�̓f�[�^�i�b�q�s����уv�����^�j �@�E���̓t�@�C���� �@�E�אڃ��X�g �E�K�w�f�[�^�\ �R�j��������Ȃ� �@�E�v�f���F�U�O�ȉ� �@�E�������C�o�����F���ꂼ��P�O�ȉ� �@�i����ӂ̐��C�o�Ă����ӂ̐��j �@�E�K�w���F�R�O�ȉ� �@�E��̊K�w�ł̗v�f���F�P�O�ȉ� �@�E���[�v�͂Q�v�f�̂݁B �S�j�s���F�V�O�i�R�����g���܂݃}���`���j �T�j���s���}1 ( ��) �Ɏ����B �v�Z���Ԃ��݂�ƁA�v�f�����P�X�łR�b�A�v�f���R�R�łT�b�ł������B
�@�v�����^FMPR-451�܂��� FMLBP112 �ɂ��K�w�}�̃��x���v�����g���s���v���O�����o�q�s�D�a�`�r���쐬�����B
�h�r�l�|�X�W�ł̃`���[�g�o�͂ł́A�v���O�����Ŏ����I�ɁA�ӂ̌����̏��Ȃ��v�f�z�u�ł̃��x���v�����g���s���Ă���B������b�r�v�f�z�u�@�ƌĂ�ł���B
�@�������A�o�q�s�D�a�`�r�͌��i�K�ł͐l��ł̔z�u�w����͂Ƃ��Ă���B�i�K�w�v�Z���ʂ̊K�w�\�Ɨאڃ��X�g���݂āA�ӂ̌��������Ȃ��Ȃ�悤�ȗv�f�̕��я����K�w���Ɏw�肷��B)
1)���̓f�[�^ �@�@5.1 �אڍs��ɂ��v���O�����i�h�r�l) �ł̓��̓t�@�C���ɁA���̂Q��̃f�[�^��lj��������̂ł���B �@�E�v�f�ԍ��Ɨv�f���i�v�f���J��Ԃ��j �@�E�K�w�� �@�@�E�K�w�ԍ��Ƃ��̊K�w�ł̗v�f�� �@�@�E�v�f�ԍ��i���̊K�w�ł̗v�f���J�Ԃ��j �@�@�@�i�����ł̗v�f�ԍ��̏��ɍ�����z�u����̂ŁA�����͕ӂ̌��������Ȃ��悤�ɁA�l���Č��߂邱�ƁB�j �Q�j�o�̓f�[�^�i�v�����^�j �@�E�K�w�} �i���f�����C�쐬���C�h�r�l�|�j�o�b����[�Ƀv�����g���A�v�f�̃��x���v�����g���K�w�����J��Ԃ��B �R�j��������Ȃ� �@�E�v�f���F�����Ȃ� �@�E�������C�o�����F���ꂼ��P�O�ȉ��i����ӂ̐��C�o�Ă����ӂ̐��j �@�E�K�w���F�����Ȃ� �@�E��̊K�w�ł̗v�f���F�W�ȉ��^�P�T��� �i�a�S�T�C�Y�c���Ȃ�T�ȉ��j �S�j�s���F�V�T�i�R�����g���܂݃}���`���j �T�j���s���}�Q�E�R�ɂ��߂��B�i���j�����̓t�@�C���ł���A�i���j���v�����g�����}�ł���B�i���x���̊Ԃ̌����́A�R���s���[�^�ł͂��Ȃ��ŁA�l���s���B�j
type ismd124.dat ISM�} 1-2 �C5 2 3, 2 4, 3 1, 3 4, 4 3, 4 5, 5 1, 0 0 1,"ismD124 �v�f���@�P" 2,"ismD124 �v�f���@�Q" 3,"ismD124 �v�f���@�R" 4,"ismD124 �v�f���@�S" 5,"ismD124 �v�f���@�T" 4, 1,1, 1 2,1, 5 3,2, 3, 4 4,1, 2
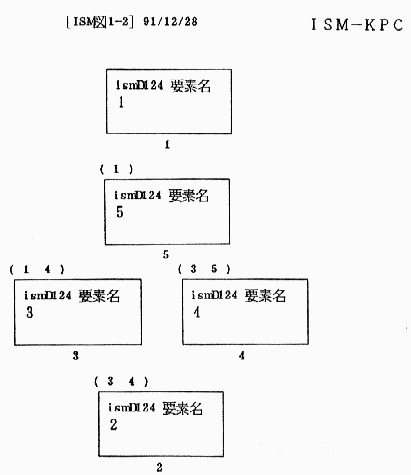
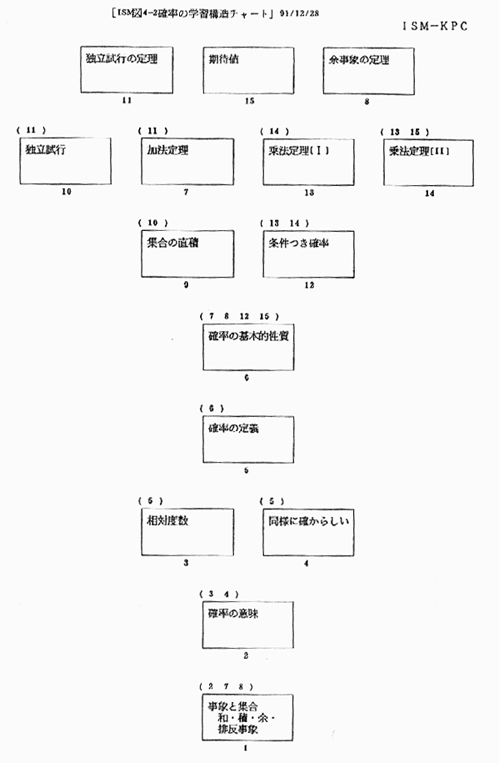
(�Q�l�����Q�̍֓����A�R�o��w�K�@�`���Z���w�Ȃ̎��H�`,pp.133�̃`���[�g�����p�j
type ismd42.dat
ISM�} 4-2�m���̊w�K�\���`���[�g �C15
1 2, 1 7, 1 8, 2 3, 2 4, 3 5, 4 5, 5 6, 6 7
6 8, 6 12, 6 15, 7 11, 9 10, 10 11, 12 13, 12 14, 13 14
14 13, 14 15, 0 0
1,"���ۂƏW���@�@�@�@�a�E�ρE�]�E�@�@�r������"
2,"�m���̈Ӗ�"
3,"���Γx��"
4,"���l�Ɋm���炵��"
5,"�m���̒�`"
6,"�m���̊�{�I����"
7,"���@�藝"
8,"�]���ۂ̒藝"
9,"�W���̒���"
10,"�Ɨ����s"
11,"�Ɨ����s�̒藝"
12,"�������m��"
13,"��@�藝�m�T]"
14,"��@�藝�m�U]"
15,"���Ғl"
8
1,3 11, 15, 8
2,4 10, 7, 13, 14
3,2 9, 12
4,1 6
5,1 5
6,2 3, 4
7,1 2
8,1 1
�P�j�K�w�v�Z�̌v�Z���Ԃ��r���Ă݂�ƁA�e�L�X�g�ł̗\�z�ǂ���ł������B�אڍs��ɂ��v�Z�́A�v�f�����傫���Ȃ�قǂ��̂Q��ɔ�Ⴕ�Ē���������̂ɑ��āA�אڃ��X�g�̕��͂��Ƃ��Ƒ�����ɗv�f���ɔ��ł��邩��A���̍����傫���Ȃ�B
�Q�j�K�w�}�̃��x���v�����g�͗v�f�z�u���w�肷��K�v������B����͎����z�u���]�܂����B
�R�j�u�f�[�^�\��II�v�̃O���t�ł̋��ނ̈�Ƃ��āA�S�D�C�T�D�P�j�̎��������ƂŐ��������B�אڍs��ɂ�鏈���菇���\���ɂ͐������Ȃ��������߂��A���邢�͂��̂悤�Ȗ��\�����K�w�}������Ӗ��̐����s�����炩�A���܂苻�����������A�������ĖႦ�Ȃ������悤�ł���B�i�A���P�[�g������ĉ�͂��ׂ��ł������B�j���̑�́A����̉ۑ�ł���B
�P�j���ނȂǂ̍\�����c�[���Ƃ��āA�h�r�l�@�̊K�w�v�Z���t�אڃ��X�g�ɂ���Č����I�ɍs���v���O�����s�n�o�n�Q�D�a�`�r���e�l�q�p�ɂe�a�g�f�C���^�v���^�Ŏ��삵�A�v�Z�ʂ̗��_�ʂ�̌v�Z���Ԃ�������Ȃ��������ʂ��B
�Q�j�K�w�}�̃v�����^�o�̓v���O�����o�q�s�D�a�`�r���쐬�������A���₷���z�u�𗘗p�҂��w�肷�邽�߂Ɏ����z�u�ɂ͂Ȃ��Ă��Ȃ��B
�R�j���p���̂��߂ɂ́A���̂悤�ȉۑ肪�c���Ă���B
���j�K�w�}�̌��₷���z�u�v�Z�̎����� ���j�g���₷���i�b�q�s�ł̊K�w�}�ȗ��\���j �@�@�@�@�@�@�@�i�v�f�ԍ��̕������j �@�@�@�@�@�@�@�i�f�[�^�Ǘ��j ���j�R�v�f�ȏ�ł̃��[�v�̏��� �@�����ɂ��āA�e�l�q�p�\�R���ł̂h�r�l�@�̃c�[���Ƃ��ĉ��P�𑱂���\��ł���B
�S�j�o�b�|�X�W�O�O�V���[�Y�p�ڐA�ɂ��ďq�ׂ�B�K�w�v�Z�̕����͂قƂ�ǂ��̂܂܂ł悢�B�v�����g�v���O�����́A�����������������ƂȂ�B
�T�j�����̍\�����c�[���𗘗p���āA�J���L�������E���ނ̍\������i�߂�B����ɁA���̑��̖��\���̔c���ɂ��K�p���A�Q���^�̃V�X�e���Y�E�A�v���[�`�������ꂽ���ƍl����B
�P�j���������C�R���Z�v�g�E�}�b�s���O�A�v���[�`�ɂ�鋳�ފJ���C�Z�\�ƋZ�p�C�P�S�W���C�����D�Q�|�V�C�P�X�X�P
�Q�j���������C�h�r�l�\���w�K�@�C�����}���C�P�X�W�V
�R�j���������C������H�w����C�����D�S�W�|�V�S�C�R���i�ЁC�P�X�W�X
�S�j�g�����j�E�֒J�����C�A�}�Ƃc�d�l�`�s�d�k�Ƃ̑g�ݍ��킹�ɂ����\���̔c���@�p�\�R�������V�X�e���r�`�l�c�h�b�|�o�C��T���v��V���|�W�E���_���W�C�����D�P�S�R�|�P�T�P�C�P�X�W�S
(2002.3.22�⑫�@�A�}�Ƃc�d�l�`�s�d�k�Ƃ̑g�ݍ��킹�ɂ����\���v�Z�iFORTRAN����j��Calcomp�v���b�^�[��}�v���O�����쐬�́A�����̈�����V�X�e���i���j�̈�v�N�ɂ��B�p�\�R���ւ̈ڐA�́A�������A�r�Y���䂳��ɂ��B�r�Y����́ANHK�e���r�́u�������{�l�v(1984.6.7)�Ŗk��B�̃\�t�g�E�F�A��Ƃ̂r�d�Ƃ��āA���̃\�t�g�̏Љ�������B���̌�A���̃e���r�ԑg�̎����҂����SAMDIC-P�̒������������B�j
�T�j���؋`��E�͑��a�F�ҁC�Q���^�V�X�e���Y�E�A�v���[�`�|��@�Ɖ��p�|�C�����D�R�R�|�V�T�C�����H�ƐV���ЁC�P�X�W�P
�U�j���{�d�C�\�t�g�E�F�A���C���ލ\���`���[�g�쐬�V�X�e���h�r�l�|�X�W�@���[�U�[�Y�}�j���A���C���{�d�C�\�t�g�E�F�A���C�P�X�W�U
�V�j�k�D�`�����������������^���R�T����C�b�|�f�[�^�\���ƃv���O�����C�����D�Q�P�R�|�Q�R�Q�C�I�[���ЁC�P�X�X�O
�W�j�������F���C�b����ɂ��ŐV�A���S���Y�����T�C�����D�P�Q�V�C�Z�p�]�_�ЁC�P�X�X�P
�@���̌�APC��MS-DOS�iBasic����Ȃ�)����Windows95�Ɉڍs�����肵�āA����Basic�v���O������������h���ʂɂ͖����Ȃ��Ă��܂����B(���ɏq�ׂ�悤�ɁAWindow���Ŏg����Basic�\�t�g���A���邢��N88�݊��̃t���[�\�t�g���g�����肷��AWindows���ł�dos basic�̎��Y���g�����Ƃ��o���邪�A��ʓI�ł͂Ȃ��B�j�@�h�r�l�@�ɂ��\���}�쐬�̕K�v���́A���낢��Ȗ�肪��蕡�G�ɂȂ��Ă��邩��A�����邱�Ƃ͂����Ă��A���Ȃ��Ȃ��Ă͂��Ȃ��B��N��́A���R���Ԃ������Ȃ�̂ŁA�N�ł�������Java�A�v���b�g�ȂǂɈڐA���Ă݂����Ǝv���B
2002.3.26 FBHG�̃\�[�X���X�g���A�b�v���[�h�����B����̎��s���Ƃ��āAMS-DOS�ŁAFBHG���N���ł���A�i�u���E�U�ł̃\�[�X�������R�s�[���ăe�L�X�g�G�f�B�^�ɓ\��t���A�g���q��bas�Ƃ��ĕۑ��������̂��j���̂܂܂ŁAload�Arun�o����BWindows���ł́AF-Basicv6.3�Ȃǂ����邪�A�����͎g���Ă��Ȃ��B
�@Windows�}�V���ł́AN88�݊�BASIC for Windows95���t���[�Ŏg����B�c�O�Ȃ���Afbhg�Ɣ�݊�������A���̂܂܂ł́A���s�ł��Ȃ�����(open�Asave�Ȃǁj������B���s���ɁA�t�@�C�������k���œ��͂��āA�f�[�^���L�[���͂ɂ��Ă��Aism.bas�Aismw.bas�ł́A���B�s���������܂�Ȃ������B�������Atopo2.bas�ɂ��ẮA���������ʂ�����ꂽ�B
�g�b�v�ɖ߂�