2001.5.21 KPC 情報技術科 関谷
回転体・柱体の独自のデータを作ることで、想像を掻き立てる立体の投影がよく分かる。形状データを変えると、いろんなイメージの回転体や、柱体になる。
プログラムを解析するには、形状データを変えるだけでなく、回転体では、稜線を表示する角度や、特定の角度の線の色を変える(柱体では、見える上(か下)の面に色を塗るとか)などの実験をしてみること
レポートには、考察として、①学習事項のまとめと②演習での結果の図をどのように作図したかを説明すること。(プログラム名やその内容、実行でのデータなど。)描画した図の中に、それらの説明を加えると,解りやすくなる。(小生が提示しているプログラムでは、出来るだけ、上部に表示するようにしている。)
画像データのファイルは、テキストデータと比較すると、相当に大きい。従って、圧縮したファイルを使うこと。圧縮は、ペイントやWordなどで、ファイルの種類を.gifや.jpg形式のファイルとして名前を付けて保存することで行う。
立体の基本図形で、比較的簡単に作れるものは、錐体、柱体、回転体がある。
回転体は、断面の2次元図形を、y軸の回りに回転させることにより生成できる。
それだけでは、複数個の楕円が描けるだけで、とても立体には見えない。そこで、断面を表す直線(稜線)をある回転角度ごとに何箇所かに描くことにする。
x軸回りの回転量-回転の向き(符号)-は関係しないことになる。(投影対象の回転体がy軸に対称なため)陰影を付けない場合、投影図からは、x軸回りの回転の向きをどちらか区別できない。
これは、回転体と違い、x軸回りの回転量-向き(符号)-は投影図で判別できる。
グラフィックスの世界を解析的に表現せず、再起的に表現する。
リカーシブ・グラフィックスのおもしろさは、驚くほど自然の形に近い図形がいとも簡単に表現でき、自然や生命の神秘的な美しさを解き明かせるのではないかという錯覚を髣髴とさせるところにある。
今回は、河西の8.2、8.3から、例題62 コッホ曲線と例題63 樹木曲線を学習する。
0次のコッホ曲線は長さlの直線である。1次のコッホ曲線は、1辺の長さがl/3の大きさの正3角形状の出っ張りを出す。2次のコッホ曲線は、1次のコッホ曲線の各辺に対し、1辺の長さがl/9の大きさの正3角形状の出っ張りを出す。これを無限回繰り返せば、無限小の長さの線分が無限本つながった曲線となる。
次数は、0から8次までの9図を3段にならべた。 このためには、window(), view()の関数を使い、繰り返しを行っている。
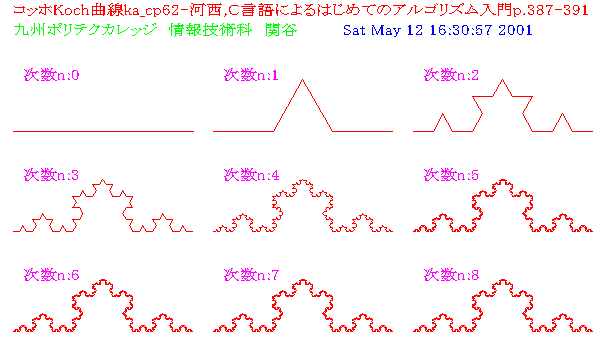
例題62 コッホ曲線を表示(1 View)
樹木曲線は、木が枝を伸ばしていく形をした図形である。
次の規則に従う。
樹木曲線は、親の枝から2本の子の枝を出していくので、2分木の木構造とまったく同じと考えることができる。
n次の木を描くアルゴリズムは次のようになる。
1)(x0,y0)から角度angleで長さlengの枝を1つ引く。引き終わった点の座標を新しい(x0,y0)とする。
2)n-1次の右部分木を再帰呼び出し
3)n-1次の左部分木を再帰呼び出し
次数n、角度branch、縮小率scaleは、キーインする。 3組をスクリーンでは、縦に並べて表示する。 3組を表示したら、色の反転をする。

例題63 樹木曲線を表示(3 View)
リカーシブ・グラフィックスのプログラムを解析しなさい。
次にそれらを改造し、皆さんの作品を作りなさい。例えば、樹木のデータ・色などを変える。配置を変える。(林になる?)
1)HtmlエディタAZUKIで、考察、ソースリストを編集した後、必要なhtmlタグを付加し、エンティティ変換などをしてhtmlファイルとして各自のMyHomeに、cg_05などの名前をつけて保存する。実行グラフィックス画面は、圧縮後のファイルをイメージのソースとして指定する。
2)情報系Webサーバにindex.htmlからのハイパーリンクを作って、登録する。概略は以下のとおり。
htmlファイルは、WordやFrontPageExpressなどで、Webページとして保存する(前述)か、AZUKIなどのエディタで必要なタグを編集する。そして、ホームページindex.htmlから、今回のレポートページへのリンクを張る。それらを各自のWebサーバのホームディレクトリの直ぐ下のpublic_htmlフォルダ(サブディレクトリ)にftpすること。